【计算机图形学基础】二射线追踪

该系列为阅读书籍Fundamentals Of Computer Graphics所做的笔记。

本篇对应书中第四章Ray Tracing。

由两种渲染方式：一种是逐个画物体；一种是逐个画像素。前者是遍历所有物体；后者是遍历所有的像素，以及影响该像素的物体。射线追踪属于后者。

关于二者的区别，在这个网站可以看到有这么一段解释：

For rendering, we need to consider all combinations of objects and pixels. This suggests a nested loop. One way to resolve the visibility is to iterate over the list of all triangles and attempt to render each one to the screen. This is called object-order rendering, and is the main topic of Section 7.2. For each triangle that falls into the field of view of the screen, the pixels are updated only if the corresponding part of the triangle is closer to the eye than any triangles that have been rendered so far. In this case, the outer loop iterates over triangles whereas the inner loop iterates over pixels. The other family of methods is called image-order rendering, and it reverses the order of the loops: Iterate over the image pixels and for each one, determine which triangle should influence its RGB values. To accomplish this, the path of light waves that would enter each pixel is traced out through the virtual environment. This method will be covered first, and many of its components apply to object-order rendering as well.

就是说imgage-order rendering逐像素渲染，外面一层的loop的对象是所有像素，里面一层的loop对象是三角形，里面一层会判断在该像素点的哪个三角形离观察者最近，并渲染它。（深度测试的原理）

基础的射线追踪算法

从观察者发送一束射线到目标像素点，命中的第一个三角形，将会被绘制。

因此一个基础的射线追踪器分为三个部分：

产生射线，决定射线的原点以及方向
射线交点，找到与射线交点最近原点的物体
绘制(shading)，绘制该交点的颜色

伪代码可以表现为

for 每个像素 do
  计算视觉射线
  找到第一个被射线击中的物体表面以及它的法向量$n$
  根据交点的法向量和光照等信息，计算出该像素点的颜色

透视

透视有很多种，比如立体透视和鱼眼透视，但是我们最常用的还是线性透视。在线性透视中，3d物体被投影到一块平面上，原来是直线的，投影完还是直线（反例是鱼眼透视，会变形）。

最简单的投影类型是平行投影，其实就是让3d物体沿着视觉平面的法向量方向运动，直到3d物体击中视觉平面。
平行投影的两种：如果图像平面正交于视觉方向，这种投影就叫正交投影，否则叫斜投影(oblique)

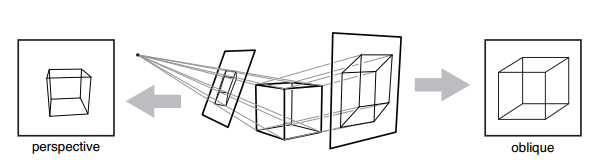
透视和平行投影不同，万物在远处会变小直至消失，平行线在远处会交汇。

计算视觉射线

一条射线的数学表达为：

$$p(t)=e+t(s-e)$$

其中，e为射线原点，s为平面上的一点。当t为0，则在e点上，当t为1，则在s点上。

正交视角

Camera Frame
在OpenGl编程里常可以看到这个词，代表相机方向和位置。

-w垂直于锥形体的上底。我们得知了点e和上底的距离d（在正交视角中，d为0，e在屏幕上），以及像素点的坐标，就可以算出射线的向量。

这里假设锥形体上底这个面中，l为屏幕左边缘的位置，右r，上t，下b。那么屏幕的大小就为(r - l) x (t - b)。

假设屏幕上一行有$n_x$个像素，一列有$n_y$行像素，那么第(i, j)个像素的坐标在u方向和v方向上的位置分别为：

$$u = l + (i + 0.5)(r - l) / n_x$$
$$v = l + (j + 0.5)(t - b) / n_y$$

那么射线就可以表达为：

射线方向 -w 平行视角，全部都是这样的

射线起点 e + $u$u + $v$v

透视视角

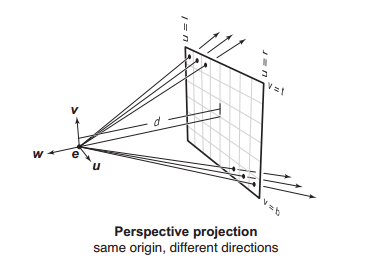
和正交视角不同，透视视角的射线为：

射线方向 -dw + $u$u + $v$v

射线起点 e

射线与物体的交汇

假设射线可以用一个一元一次方程表达（类似于y = b + kx)，表示为 p(t) = e + td，求它跟面f(p) = 0的交点。

射线与球的交点

设球的重点为c，球可以表示为

$$(x - x_c)^2 + (y - y_c)^2 + (z - z_c)^2 - R^2 = 0$$

把它写成向量的形式就是

$$\textbf{(p - c)(p - c)} - R^2 = 0$$

其中，p为球面上的一点。如果我们把射线方程中的p带入到球的向量表达式中，可以得到

$$(\textbf{e} + t\textbf{d} - \textbf{c})^2 - R^2 = 0$$

拆出来得到一个关于$t$的二元一次方程：

$$(\textbf{d}\cdot\textbf{d})t^2 + 2\textbf{d}\cdot(\textbf{e} - \textbf{c})^t + (\textbf{e} - \textbf{c})^2 - R^2 = 0$$

最后根据二元一次方程的解法算出$t$。

射线与三角形的交点

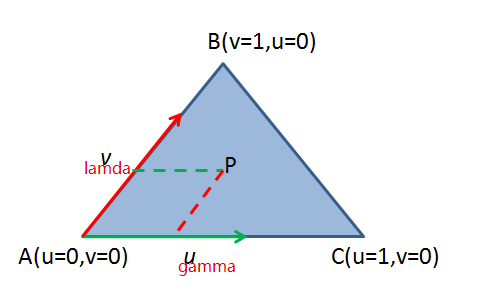
先复习一波重心法

三角形中的任意两个顶点，可以由第三个顶点的位移来表示。
如果一个点$\textbf{P}$在三角形内，那么它可以表示为
$$\textbf{P} = \textbf{A} + \gamma(\textbf{C} - \textbf{A}) + \lambda(\textbf{B} - \textbf{A})$$
并且要求：
$$\left\{
\begin{aligned}
\lambda \gt 0 \\
\gamma \gt 0 \\
\lambda + \gamma \lt 1
\end{aligned}
\right.$$

可以看到，当$\lambda$为1，$\gamma$为0时，点在$\textbf{B}$上，当$\lambda$为0，$\gamma$为1时，点在$\textbf{C}$上。所以必须符合$\beta + \gamma \lt 1$

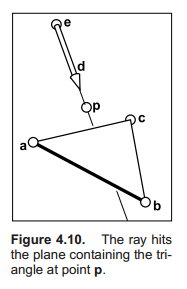
检测射线与三角形交点的方法有很多，这里使用重心法。

要求解出

$$\textbf{e} + t\textbf{d} = \textbf{f}(u, v)$$

其中，等式右边表示在三角形上的点。

这条等式又可以表达为：

$$\left\{
\begin{aligned}
x_e+tx_d=f(u,v) \\
y_e+ty_d=g(u,v) \\
z_e+tz_d=h(u,v)
\end{aligned}
\right.\tag{1}
$$

在上式中，我们有3条等式和3个未知数$t, u, v$。现在已知三角形的三个点$\textbf{a}$、$\textbf{b}$和$\textbf{c}$。

这就得到：

$\textbf{e} + t\textbf{d} = \textbf{a} + \beta(\textbf{b} - \textbf{c})) + \gamma(\textbf{c} - \textbf{a})$ 式子一

为了解出$t,\,\beta,\,\gamma$，我们把(1)拆开得到：

$$x_e + tx_d = x_a + \beta(x_b - x_a) + \gamma(x_c - x_a)$$
$$y_e + ty_d = x_a + \beta(y_b - y_a) + \gamma(y_c - y_a)$$
$$z_e + tz_d = x_a + \beta(z_b - z_a) + \gamma(z_c - z_a)$$

写成向量的形式：

$$
\left[
\begin{matrix}
x_a - x_b & x_a - x_c & x_d \\
y_a - y_b & y_a - y_c & y_d \\
z_a - z_b & z_a - z_c & z_d
\end{matrix}
\right]
\left[
\begin{matrix}
\beta \ \gamma \ t
\end{matrix}
\right]
=
\left[
\begin{matrix}
x_a - x_e \\
y_a - y_e \\
z_a - z_e \\
\end{matrix}
\right]
$$

接下来使用克莱姆法则(Cramer’s Rule)来解决这个问题。

？？？克莱姆法则又是啥玩意儿？

摔！！！

好的总之最后就得到了$t,\,\beta,\,\gamma$关于几个已知点的表达式。

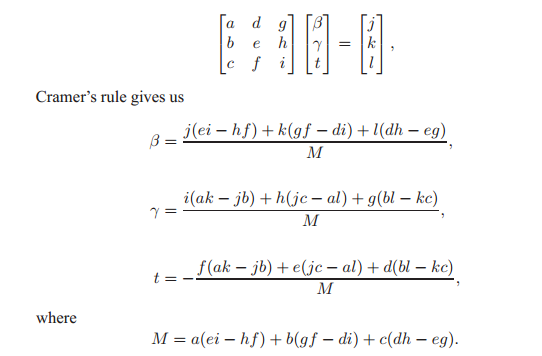
现在只需要判断他们是否符合几个条件，就可以直到交点在不在三角形内了。伪代码为

$
compute\,t \\
\textbf{if} \, (t \lt t_0) \, or \, (t \gt t_1) \, \textbf{then} \\
\quad \textbf{return} \, false \\
compute\,\gamma \\
\textbf{if} \, (\gamma \lt 0) \, or \, (\gamma \gt 1) \, \textbf{then} \\
\quad \textbf{return} \, false \\
compute\,\beta \\
\textbf{if} \, (\beta \lt 0) \, or \, (\beta \gt 1 - \lambda) \, \textbf{then} \\
\quad\textbf{return} false \\
\textbf{return}\,true
$

与一组物体相♂交

hit = false
for o in group do
  if (o is hitAtParamT and (t >= t0 and t<= t1)) then
    hit = true
    hitobject = o
    t1 = t -- 不断缩小范围
return hit

着色

一旦知道一个像素点上要绘制的物体，就开始着色啦。

大多数模型是来模拟光照效果的。对于一个光照模型中，决定性因素有如下：

光线方向 l 这是一个指向光源的单位向量
视觉方向 v 指向相机的单位向量
法向量 n
颜色等等的表面信息

Lambertian着色

在18世纪提出来的最简单的光照模型。

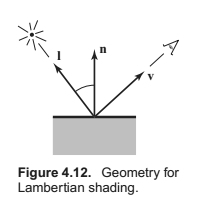
这里假设表面法向量与光向量的夹角为$\theta$，$k_d$为一个系数。那么，光强L等于

$$L = k_dI\text{max}(0, \textbf{n}\cdot\textbf{l})$$

其中，$L$是像素的颜色；$k_d$是漫反射系数，或者说表面颜色；$I$是光源的光强。由于n和l都是单位向量，所以我们可以把$\textbf{n}\cdot\textbf{l}$速记成$\cos\theta$。l很容易计算，我们从上一节中知道了如何计算出视线与表面的交点，算出交点之后用光源坐标减去交点坐标，再正规化即可。

可以表达为：

光强 = 因子 x 光照强度 x (法向量与光线的夹角程度)

最重要的是后面粗体部分。

我们可以分别对RGB三个颜色通道，使用这条公式得出结果。

Blinn-Phong着色

Lambertian着色是视角无关的，不管相机在哪个相对位置，看到的颜色都是一样的，这种着色法没办法产生高光。现在有很多着色模型把Lambertian着色作为漫反射部分，再添加一个镜面反射部分。

Blinn-Phong光照模型中，当v和l关于法向量对称的时候，将看到最大亮度，也就是能看到镜面反射。随着v离该方向越远，光强会慢慢下降。

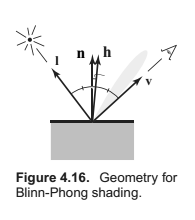
现在沿着假定v和l夹角的等分线方向，有个单位向量h。当n与h重叠的时候，l与v将关于n对称。当$\cos \gamma$的值（这里假设$\gamma$为n与h的夹角）越小，光强越大。这里再给他们定一个幂数p，让镜面反射的衰变能够来得更猛烈一点（也就是p越大，光斑的面积会越小）。

我们可以计算出h

$$\textbf{h}=\frac{\textbf{v} + \textbf{l}}{| \textbf{v} + \textbf{l} |}$$

最后得到光照强度：

$$L = k_dI\text{max}(0, \textbf{n}\cdot\textbf{l}) + k_sI\max(0, \textbf{n} \cdot \textbf{h})^p$$

环境光着色

Ambient Shading.

现在再多考虑一个环境光，也就是本光源以外的所有光源总和。考虑环境光是为了避免在本光源照不到的地方，乌漆嘛黑一片的巨丑。

$$L = k_aI_a + k_dI\text{max}(0, \textbf{n}\cdot\textbf{l}) + k_sI\max(0, \textbf{n} \cdot \textbf{n})^p$$

多光源光照

把结果都加起来即可

$$L = k_aI_a + \sum_{i=1}^{N}k_dI\text{max}(0, \textbf{n}\cdot\textbf{l}_i) + k_sI\max(0, \textbf{n} \cdot \textbf{h}_i)^p$$

阴影

考虑进阴影之后，逻辑就变成：

如果被光源直射，没有遮挡，那么用Blinn-Phong模型，如果被遮挡了，那么只有环境光。

理想的镜面反射

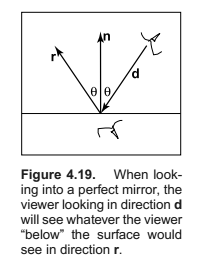
得到：

$$\textbf{r} = \textbf{d} - 2( \textbf{d} \cdot \textbf{n}) \textbf{n}$$

真实世界中，发生反射的时候会丢失部分能量，而且不同颜色丢失的能量不同。所以：

$\text{color}\,c = c + k_m \text{raycolor}(\textbf{p} + s\textbf{r}, \epsilon, \infty)$

其中，$k_m$是一个镜面RGB颜色。

【计算机图形学基础】二 射线追踪