【计算机图形学基础】5 Pipeline

发表于 | 分类于 | 阅读次数:

【计算机图形学基础】5 Pipeline

该系列为阅读书籍Fundamentals Of Computer Graphics所做的笔记。

本篇对应书中第八章 The Graphics Pipeline。

看过好几次的渲染管线。

object-order rendering其实分为硬件和软件两种，硬件的高效一些，用于实时渲染，api比如OpenGL和DirectX；软件的注重质量，比如RenderMan。但是两者用的渲染管线结构都差不多。

渲染管线的起点是object，终点是更新图像中的像素点。

先贴图

光栅化

由于前面几章已经讲过Vertex Processing阶段的矩阵变换了，这篇就从第二阶段的光栅化讲起。

写过shader的同学都知道，顶点着色器的输入和输出都是顶点，而像素着色器的输入却是fragment。怎么从顶点着色器输出的几个顶点，变成几何面上拥有的所有像素呢？这个转化的过程就叫做光栅化。

光栅器接收顶点和其他顶点着色器输出信息作为参数，输出fragments。fragment包含一个像素里所有的信息，这些信息是顶点着色器输出信息的插值版本。

光栅器的工作有二：

  • 枚举出几何体所包含的所有像素
  • 对顶点着色器的输出做插值

理解梯度

首先要复习一下$\nabla$(nabla)算子，也叫向量微分算子。定义为$\nabla = \frac{d}{dr}$。在n维空间中有不同的表现。
在三位情况下，$\nabla = \frac{\partial}{\partial x}i + \frac{\partial}{\partial y}j + \frac{\partial}{\partial z}k$ 或 $\nabla = (\frac{\partial}{\partial x},\frac{\partial}{\partial y}, \frac{\partial}{\partial z})$

梯度是啥呢？
假设三维空间中有个映射$f(x,y,z)$，则在某个点$(x, y, z)$上，梯度表示该点的一个方向，往这个方向移动，$f()$的变化最大。如果假设$f(x, y, z)$是某个山坡的表面，那么梯度就是该点上最抖的方向，梯度的大小代表有多抖。

一个标量函数的梯度记为$\nabla \varphi$，再三维直角坐标中
$$\nabla \varphi = (\frac{\partial \varphi}{\partial x},\frac{\partial \varphi}{\partial y}, \frac{\partial \varphi}{\partial z})$$

剩下的就是对每个维度求导数了。

譬如对于$\varphi = 2x + 3y^2 - \sin(z)$，梯度为

$$\nabla \varphi = (\frac{\partial \varphi}{\partial x},\frac{\partial \varphi}{\partial y}, \frac{\partial \varphi}{\partial z}) = (1, 6y, -\cos(z))$$

画线

根据线的两点式，可以推断出线的表达式

$$f(x,y) \equiv (y_0 - y_1)x + (x_1 - x_0)y + x_0y_1 - x_1y_0 = 0$$

假设$x_0 \leq x_1$，那么斜率m为

$$m = \frac{y_1 - y_0}{x_1 - x_0}$$

下面仅考虑$m \in [0, 1)$的情况。

为了光栅化，现在先确定线的开头和结尾在哪个像素点，设线的左边在$(x_0, y_0)$，线的右边末端在$(x_1, y_1)$，那么光栅化算法大概是这样

1
2
3
4
5
y = y0
for x = x0; x1 do
    draw(x, y)
    if (some condition) then
        y = y + 1

其中的x和y都是整数。
简而言之，从最左边开始遍历，往右水平地选择（保持y相同）像素，当遇到某种情况的时候把y提高一。关键就是要找到这个某种情况是什么。

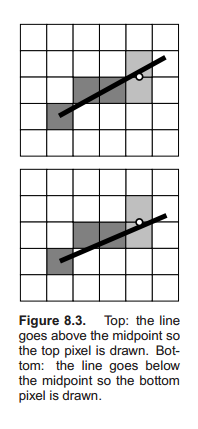
决定要不要y+1很简单。首先取两个可选择的潜在像素的中点，然后判断线在这个中点之上还是之下。如果在这个中点之上，则y+1，否则保持y。接下来就是根据高中的数学知识，只要$f(x) \lt 0$，那么点就在线的下面，要上移一个y；反之点在线的上面，保持y不变。

如果需要更高性能的表现，就要使用更高效的方法。

以下结论基于我们两个推导（很简单，自己相减就能得到$\delta$）。

$$f(x + 1, y) = f(x, y) + (y_0 - y_1)$$
$$f(x + 1, y + 1) = f(x, y) + (y_0 - y_1) + (x_1 - x_0)$$

1
2
3
4
5
6
7
8
9
y = y0
d = f(x0 + 1, y0 + 0.5)
for x = x0; x1 do
    draw(x, y)
    if d < 0 then
        y = y + 1
        d = d + (x1 - x0) + (y0 - y1) -- d = f(x + 1, y + 1) = f(x, y) + (y0 - y1) + (x1 - x0)
    else
        d = d + (y0 - y1) -- d = f(x + 1, y) + (y0 - y1)

$f(x + 1, y)$和$f(x + 1, y + 1)$的推导可以自己验证。由于后面那一串都是常数，对常数做加法是很快的。
为啥这么算更快呢？其实判断也是基于上面的基础结论，就是判断中点于$f(x, y)$的结果与0做比较。由于我们的线是一条直线，是线性的，所以可以在一开始算出$x+1$的中点值，后面x步进1，y看情况要不要步进1，就可以算出$x+1$时$f(x, y)$的值。这样就避免了每次去计算$f(x, y)$的值，每次要计算的结果都可以在上一个结果加一个常数来计算，大大提高了速度。

三角形光栅化

主要是要考虑插值问题。假设三角形三个点的颜色分别是$\textbf{c}_0$、$\textbf{c}_1$、$\textbf{c}_2$，那么三角形内某个点的颜色应该是

$$\textbf{c} = \alpha \textbf{c}_0 + \beta \textbf{c}_1 + \gamma \textbf{c}_2$$

其中的$(\alpha, \beta, \gamma)$是重心坐标。

重心坐标

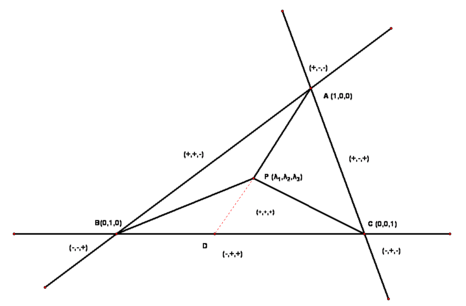
也叫面积坐标。我们用黑体小写字母表示对应点的向量。假设三角形被点$\textbf{p}$分割为三个小三角形，它们的面积之比为$\lambda_1 : \lambda_2 : \lambda_3$，且$\lambda_1 + \lambda_2 + \lambda_3 = 1$

首先BD:DC = $\lambda_3 : \lambda_2$。这个结论怎么出来的呢：
$$\frac{\triangle ADC}{\triangle ADB} = \frac{\triangle PDC}{\triangle PDB} = \frac{DC}{BD}$$
得到
存在一个$\lambda$使得：
$$\triangle ADC = \lambda \triangle PDC$$
$$\triangle ADB = \lambda \triangle PDB$$
得到：
$$\frac{\lambda_2}{\lambda_3} = \frac{\triangle APC}{\triangle APB} = \frac{\triangle ADC - \triangle PDC}{\triangle ADB - \triangle PDB} =\frac{\lambda \triangle PDC - \triangle PDC}{\lambda \triangle PDB - \triangle PDB} = \frac{(\lambda - 1) \triangle PDC}{(\lambda - 1)\triangle PDB} = \frac{\triangle PDC}{\triangle PDB} = \frac{DC}{BD}$$

根据
$$\frac{\textbf{d} - \textbf{b}}{\textbf{c} - \textbf{d}} = \frac{\lambda_3}{\lambda_2}$$
可以求得$\textbf{d}$关于$\textbf{b}$和$\textbf{c}$的等式：
$$\textbf{d} = \frac{\lambda_2 \textbf{b} + \lambda_3 \textbf{c}}{\lambda_2 + \lambda_3}$$
现在已知点A和点D了，准备从A和D身上计算出点P的向量。

没耐心看完上面论证的胖友，知道一点就好：点p在跟三个点的连线把三角形分为三个小的三角形，三个三角形的面积之比为$\lambda_1 : \lambda_2 : \lambda_3$，且$\lambda_1 + \lambda_2 + \lambda_3 = 1$，那么，这个三角形关于三个顶点的表达式为$\textbf{p} = \lambda_1 \textbf{a} + \lambda_2 \textbf{b} + \lambda_3 \textbf{c}$，这就是它的重心坐标。

根据这点，假设有线性函数F，输入为顶点，输出为颜色。已知ABC三点的颜色为xyz，那么：
$$F(A) = x$$
$$F(B) = y$$
$$F(C) = z$$
对于点p来说
$$F(P) = F(\lambda_1 \textbf{a} + \lambda_2 \textbf{b} + \lambda_3 \textbf{c}) = \lambda_1 x + \lambda_2 y + \lambda_3 z$$

另一个问题。

有时候画相邻的两个三角形，会修改共用边的颜色多次。为了避免这样，重心法只用在三角形内部的点。

计算出点的重心坐标很简单，只要符合下面三条式子即可求出三个未知数

$$\alpha x_A + \beta x_B + \gamma x_c = x_p$$
$$\alpha y_A + \beta y_B + \gamma y_c = y_p$$
$$\alpha + \beta + \gamma = 1$$

画出一个三角形的伪代码：

1
2
3
4
5
6
for all x do
    for all y do
        compute (alpha, beta, gamma) for (x, y)
        if(alpha in [0, 1] and beta in [0, 1] and gamma in [0, 1]) then
            c = alpha * cA + beta * cB + gamma * cC
            drawpixel(x, y) with color c
Buy Me A Coffee / 捐一杯咖啡的钱
分享这篇文章~
0%
//