【计算机图形学基础】四 Viewing
该系列为阅读书籍Fundamentals Of Computer Graphics所做的笔记。
本篇对应书中第七章四 Viewing。
这篇讲的是如何把3d物体映射成2d的,也就是投影。
第四章的射线检测讲了那么多,现在都是没人用了的,现在基本都在顶点着色器那里直接用投影矩阵给投影了。
Viewing Transformations
对应矩阵名称MVP,是最后阶段的变换。
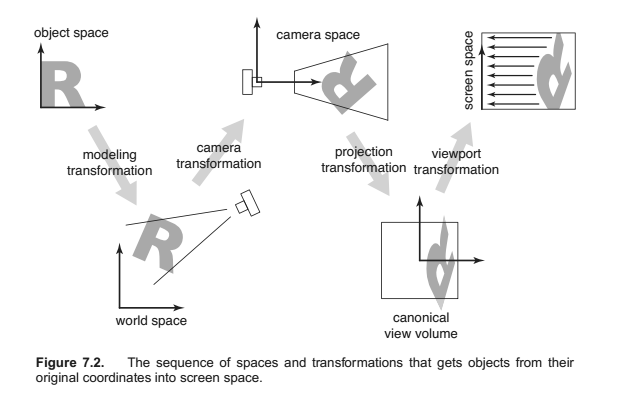
一般来说要投影到屏幕上,一系列的变换:
- 一个相机变换
- 一个投影变换
- 一个窗口变换
一个物体首先要把自己的旋转和位置转换成相对于世界的,这一步叫modeling变换;然后,再进行相机变换,转换到以相机位置为原点的坐标系上;然后使用投影矩阵进行投影到一个单位矩形内;最后,把单位矩形映射成屏幕坐标。
The Viewport Transformation
视窗变换。
把$(x, y, z) \in [-1, 1]^3$的矩阵转换到分辨率为$n_x \times n_y$的屏幕上。变换由两部分组成:
- 缩放 矩阵$\hat{S}$代表
- 位移 矩阵$\hat{T}$代表
$$\mbox{${\mathbf{\hat{S}}}$}=\left(\begin{array}{ccccc}
\frac{v_r-v_l}{2}&0&0&0 \\
0&\frac{v_t-v_b}{2}&0&0 \\
0&0&\frac{1}{2}&0 \\
0&0&0& 1 \end{array} \right)$$
$$\mbox{${\mathbf{\hat{T}}}$}=\left(\begin{array}{ccccc}
1&0&0&\frac{v_r+v_l}{2}\\
0&1&0&\frac{v_t+v_b}{2}\\
0&0&1&\frac{1}{2}\\
0&0&0&1 \end{array} \right)$$
相乘得
$$\mathbf{\hat{V_p}}=\mathbf{\hat{T}}\mathbf{\hat{S}}
=\left(\begin{array}{ccccc}
\frac{v_r-v_l}{2}&0&0&\frac{v_r+v_l}{2}\\
0&\frac{v_t-v_b}{2}&0&\frac{v_t+v_b}{2}\\
0&0&\frac{1}{2}&\frac{1}{2}\\
0&0&0&1 \end{array} \right)$$

