【计算机图形学基础】6 表面渲染
本篇也可改名给大家看的图形学趣味基础23333.
该系列为阅读书籍Fundamentals Of Computer Graphics所做的笔记。
本篇对应书中第十章 Surface Shading。
第九章是离散数学,实在是懒得啃了,傅里叶变换那一套。
本章探讨比较有启发性的三种着色:漫反射着色、Phong着色、艺术着色。
Diffuse Shading
用来着色无光泽的表面。
Lambertian着色模型
一个Lambertian物体遵守Lambert的cos法则。
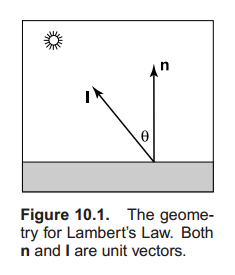
$$c \propto \theta$$
也就是
$$c \propto \textbf{n} \cdot \textbf{l}$$
有两个因素可以决定表面的明亮:光照强度和表面的反射率。反射率也是由RGB组成的。假设物体的漫反射颜色比较接近红色,那么反射率中R的那部分就要大一些。于是可以把式子改写成这样:
$$c \propto c_r \textbf{n} \cdot \textbf{l}$$
为了保证输出的表面颜色值的RGB均属于[0, 1]的范围,需要让光照强度也属于[0, 1]。式子加上光强之后就变成:
$$c = c_r c_l \textbf{n} \cdot \textbf{l}$$
这是一个形式很简单的式子,但是有可能输出不在[0, 1]范围内的RGB值,只因点乘的结果可能是负数。为了避免结果出现西安负数,还需要加一个取max值的操作。
$$c = c_r c_l \max(0, \textbf{n} \cdot \textbf{l})$$
环境光着色
在真实世界中,往往除了我们所给的光源,还有环境光存在。我们不用考虑方向,把它整个叠加上去就行了。得到:
$$c = c_r (c_a + c_l \max(0, \textbf{n} \cdot \textbf{l})), c_a + c_l \leq (1, 1, 1)$$
基于顶点的漫反射着色
想象一个三角形,如果只对中间某个点计算颜色并应用到整个三角形,就会让一个由多个三角形组成的平面看起来很粗糙(区分得出各个三角形,边界may be非常明显)。
为了避免上述情况,我们把三角形的法向量应用到它三个点上,求得三个点的颜色之后再来做插值。
当然,更好更细腻的着色是把光照直接放到fragment shader里头去,针对每个像素做着色处理,不过这非常非常消耗性能。
Phong着色
现在考虑一些有高光反射的表面。我们可以观察到高光的位置会随着我们眼睛的位置移动,并且高光的颜色一半就是光源的颜色,和物体本身的颜色无关。另外,高光一般来说会有某种程度的blur(模糊),这就需要一个模糊半径。所以在式子里我们要多加入一个向量e表示眼睛。
Phong光照模型

图中,r为l关于法向量n对称的向量。当人眼e越接近r,看到的镜面反射光强就越大。
给出向量r,为了能让e = r的时候最亮,且e远离r的时候可以逐步变暗。可以简单地产出这么个式子:
$$c = c_l (\textbf{e} \cdot \textbf{r})$$
但是这个式子有两个问题。一个是点乘的结果有可能是个负数,这个还好,可以通过绝对值或者取max之类的解决。另一个问题是,这个式子产出的光斑面积要比现实中的大太多,显得不自然。
为了解决光斑太大的问题,我们给点乘的结果加上一个幂数。结合max得到以下式子:
$$c = c_l \max(0, \textbf{e} \cdot \textbf{r})^p$$

上式中的p被称为Phong指数,它是一个正实数。

为了完成上式,我们必须要先知道r,根据上图,它可以被这么算出:
$$\textbf{r} = -\textbf{l} + 2(\textbf{l} \cdot \textbf{n})\textbf{n}$$
其中的$\textbf{l} \cdot \textbf{n} = \cos \theta$。
有一种近似的算法,可以避免算出r。我们现在要计算l与e的中间单位向量h(half)。
$$\textbf{h} = \frac{\textbf{e} + \textbf{l}}{|\textbf{e} + \textbf{l}|}$$
当h与n重合的时候,光斑达到最大亮度。于是:
$$c = c_l(\textbf{h} \cdot \textbf{n})^p$$
这个式子还能少了一个max操作,hin完美。如果想把镜面反射变得再暗一点,还可以添加一个因子$c_p$。
最后,结合漫反射,得到式子为:
$$c = c_r(c_a + c_l\max(0, \textbf{n} \cdot \textbf{l})) + c_l c_p(\textbf{h} \cdot \textbf{n})^p$$
艺术着色
轮廓着色
当两个三角形共用一条边,且一个三角形看得到,一个三角形看不到的时候,就应该把这条轮廓画下来。这一条件可以表达为:
$$(\textbf{e} \cdot \textbf{n}_0)(\textbf{e} \cdot \textbf{n}_1) \leq 0$$

