【计算机图形学基础】7 纹理映射

该系列为阅读书籍Fundamentals Of Computer Graphics所做的笔记。

本篇对应书中第十一章 Texture Mapping。

对于无图案的表面，漫反射只需一个$c_r$，而对于一个有着复杂图案的表面，光一个单一值得$c_r$是无法满足需求的。为了能够显示出图案来，我们把反射信息储存在图像中，然后把它映射到表面。这个技术就叫做纹理映射。

这里会先讲3D纹理，也叫solid textures或volumn textures。再讲2d纹理，也叫image textures。不过如果我们纹理一词没有加上个2d或者3d的前缀，那一般指的就是2d的纹理。

2d纹理和3d纹理的区别

3D texture works like regular texture. But it is truly 3D. 2D textures has UV coords, 3D has UVW (you had to use them propably). Texture coords are unit cube (0 - 1, 0 - 1, 0 - 1).

Possible usage:

volumetric effects in games (fire, smoke, light rays, realistic fog)
caching light for realtime global illumination (CryEngine for example)
scientific (MRI, CT scans are saved into volumes)
Performance:
Same as regular texture - super fast (fastest memory access in gpu). Cached for threads and optimized for the situation when near threads (pixel shaders) are looking for near values.

Can be read as point or used linear sampling (native tri-linear interpolation. Eq bi-linear interpolation in 2D texture).

They are stored in memory like a array of 2D textures.

另可见Introduction To Textures in Direct3D 11。

说了这么多，其实下面说的3d texture mapping并不是在讲3d纹理，是在讲怎么给3d物体做纹理映射（摔(′д｀ )…彡…彡我特码…）

3D上的纹理映射

3D纹理的一般作用：

CT扫描出来的立体图像
游戏中的火焰或者烟雾
游戏中的草地

上集节目中我们提到我们用$c_r$来代表表面的颜色。而拥有复杂图案的表面，其上的颜色肯定不止一种。为了表示表面的颜色，我们使用关于p点的函数$c_r(\textbf{p})$。

3d条纹纹理

有很多种方法可以弄出一个条纹纹理。假设我们有两种颜色$c_0$和$c_1$要来组成条纹纹理。我们可以使用sin的方法来生成纹理：

function stripe(p)
    if sin(p.positionX) then
        return c0
    else
        return c1

为了调节条纹的宽度，我们可以控制一下sin的频率，加入因子$\omega$：

function stripe(p, omega)
    if sin(pi * p.positionX / omega) > 0 then
        return c0
    else
        return c1

如果我们想对条纹做模糊化，就要做插值，插值的算法如下：

1
2
3

function stripe(p, omega)
    t = (1 + sin(pi * p.positionX / omega)) / 2
    return (1 - t) * c0 + t * c1

我不知道这节有什么用。。真有人会去生成条纹嘛，做斑马？

纹理数组

假设纹理的大小是$n_x \times n_y$，另有屏幕上对应像素点坐标ij的uv坐标。那么对于某个uv坐标，它的颜色是：
$$c(u, v) = c_{ij}$$

, where

$$i = \text{floor}(un_x)$$
$$j = \text{floor}(vn_y)$$

为了有一个更smooth的效果，可以使用双线性插值，计算公式如下：

$$c(u,v) = (1 - u’)(1 - v’)c_{ij} \\

u’(1 - v’)c_{(i + 1)j} \\
(1 - u’)v’c_{i(j + 1)} \\
u’v’c_{(i + 1)(j + 1)}$$

where

$$u’ = n_xu - \text{floor}(n_xu)$$
$$v’ = n_xv - \text{floor}(n_yv)$$

好了，细节就不用懂了，skip，skip。

另外还有一种叫hermite插值的，也不讲了，感觉以后也没啥机会写这个…

生成噪点

这节讲怎么生成能看的随即图，也不看。

2D纹理映射

怎么得出一个球的uv坐标呢（所以本节为什么考虑个球呢？）？首先要给出球面上xyz点的表达式，进而推导出它的极坐标，再由极坐标计算出uv（为什么呢？）

首先，xyz：

$$x = x_c + R\cos\phi\sin\theta$$
$$y = y_c + R\cos\phi\sin\theta$$
$$z = z_c + R\cos\theta$$

从而得到极坐标$(\theta, \phi)$：

$$\theta = \arccos(\frac{z - z_c}{R})$$
$$\phi = \arctan2(y - y_c, x - x_c)$$

由于$(\theta, \phi) \in [0, \pi] \times [-\pi, \pi]$，所以我们要把它转化到$[0, 1]^2$域，从而得到uv。

$$u = \frac{\phi}{2\pi}$$
$$v = \frac{\pi - \theta}{\pi}$$

看到这里，结合前文，明白了两个道理：

为什么说给3d纹理映射更简单呢，这是建立在3d纹理由一个一个小平面组成的基础上
2d纹理映射的意思是映射到一个曲面上

对三角形的纹理映射

回忆起三角形中一个点p的重心坐标$(\beta, \gamma)$：

$$\textbf{p}(\beta, \gamma) = \textbf{a} + \beta(\textbf{b} - \textbf{a}) + \gamma(\textbf{c} - \textbf{a})$$

根据以前某个篇章的推论，我们可以由重心坐标和三个点的uv得到p点的uv。

$$u(\beta, \gamma) = u_a + \beta(u_b - u_a) + \gamma(u_c - u_a)$$
$$v(\beta, \gamma) = v_a + \beta(v_b - v_a) + \gamma(v_c - v_a)$$

其实这个操作我们写shader的人根本不需要关心，三角形各种属性（包括颜色，uv，法向量等等）的插值都是在光栅化阶段做的事情，传输到fragment shader的uv已经是被插♂值的了。

透视下的纹理映射

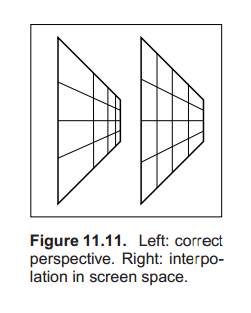
太复杂了有空再看，TODO一下。

生成隆♂起

这节讲的是怎么生成星球表面那种隆起。

怎么办呢？我不想看，跳过。

位移映射

上一节生成的隆起既不能产生阴影，又不能改变物体的轮廓，因为我们根本就没有改变这个几何体，只是生成了纹理。

其实就是生成新的p’。

$$\textbf{p}’ = \textbf{p} + f(\textbf{p})n$$

就是说让点p沿着它的法向量的方向位移一定距离，这样子就真的可以形成一个隆起。

环境映射

这节讲的是cube map。

最基础的想法就是立方体贴图的是一个无限大的cube，每个面都有纹理。因为立方体很大，所以从每个角度看到的景色都是一样的。所以给定一个方向b，就可以决定它所对应的uv是什么。

具体的方法就不看了，有空再去查天空盒相关的知识吧。