【计算机图形学基础】8数据结构

发表于 | 分类于 | 阅读次数:

【计算机图形学基础】8数据结构

该系列为阅读书籍Fundamentals Of Computer Graphics所做的笔记。

本篇对应书中第十二章 Data Structures for Graphics。

主要讲几种比较实用的数据结构：网格、空间数据、场景图形。

三角网格

每个顶点的数据通常要包含：位置、颜色、法向量、反射率等。

网格拓扑

The idea that meshes are surface-like can be formalized as constraints on the mesh topology—the way the triangles connect together, without regard for the vertex positions.

喵喵喵？

首先要通俗地讲一下啥是流形(manifold)。

quora上有解释如下：

A manifold in a three dimensional space can be imagined as a surface. More generally, a manifold embedded in $n -1$ dimensional euclidean space locally looks like a $n−1$-dimensional vector space. For example Earth (a big sphere) is a big manifold embedded in 3-dimensional space. But, we as tiny entities living on its surface can only see flat 2-dimensional land. So locally at every point on a sphere, it looks like a 2-dimensional plane.

Curves in 3-dimensional space are also manifolds. But, they locally look like 1-dimensional vector space(a line). To be a little more precise, a manifold embedded in n-dimensional euclidean space locally looks like k-dimensional vector space $(k \lt n)$ at every point on it.

A manifold has a dimension.

A 2-dimensional manifold is a surface. It could also be a union of several surfaces, too. But I’ll assume the manifolds we’re talking about are connected for the rest of this explanation.

A 1-dimensional manifold is a curve.

A 0-dimensional manifold is a point.

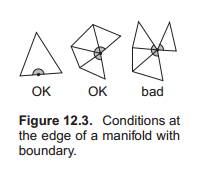
很多算法都假设网格是流形的。为了避免程序崩溃，程序会检查以下两点来确保网格是流形：

  • 每条边只被两个三角形共享
  • 每个顶点周边都环绕有一连串不间断的三角形（一个接一个，不间断）

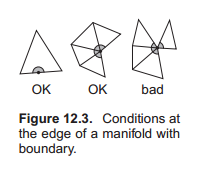
由于有时候我们游戏中的表面并不是闭合的，也就是相当于表面是有边缘的，这并不符合上面的规定，所以我们把这规定松动一下：

  • 每条边被一个或者两个三角形使用
  • 每个顶点都被连接到一个边练边的三角形集合(Every vertex connects to a singl edge-connected set of triangles.)

最后一点要注意的是三角形的正反面，或者叫内外侧，由顶点的顺序决定。逆时针方向(counterclockwise order)为正面，反之为反面（可能某些另外的系统定义会反过来）。一个连接网格(connected mesh)要保证上面所有相邻的三角形都是一个转向的。在两个转向一致的共享同一条边的三角形中，构成这条边的两个点在两个三角形中出现的次序是相反的。

Indexed Mesh Storage

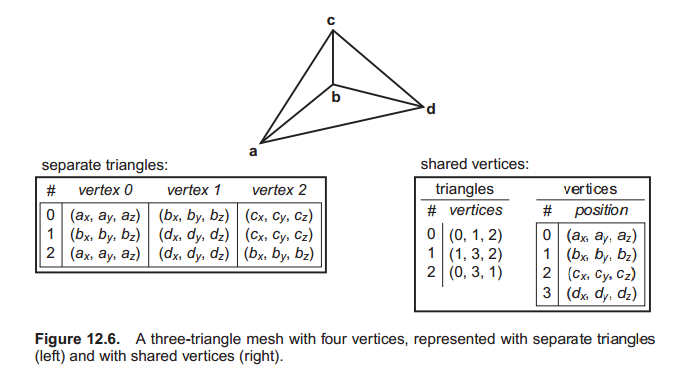
为了省空间，一般采用上图中右边那种方法：每个三角形只储存顶点的索引，或者说指针。

代码可以是这么写：

1
2
3
4
5
6
7
8
class Vertex {
    vector3 position;
    // other vertex data like color
};

class Triangle {
    Vertex v[3];
};

或者可以这么定义一个网格：

1
2
3
4
class IndexedMesh {
    int triangleIdx[nTriangles][3]
    vector3 verts[nVertices]
};

Triangle Strips and Fans

讲两种组织方式，在OpenGL编程里可以看到。

使用strips和fans两种组织方法可以更有效率。

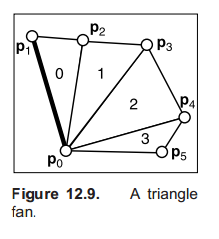
fan方法以顶点0为共用顶点。

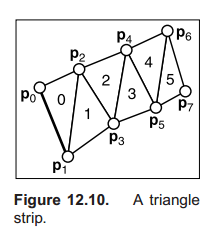
strip通常用来组成带♂状♂物。顺序是(0, 1, 2)(2, 1, 3)(2, 3, 4)(4, 3, 5)。总之就是对这个带状物上面一条边的顶点遍历，对找没绘制过的从这个点开始的逆时针构成的三角形。

Data Structures for Mesh Connectivity

索引网格、带、扇都是挺不错的紧凑网格结构。但是这些结构很难更改网格。为了能够高效地更改网格数据，需要用更复杂的结构。目的是解决这些问题：

  • 给出一个三角形，它的三个相邻的三角形是哪三个
  • 给出一个边，哪两个三角形在用它
  • 给出一个顶点，哪些面在用它
  • 给出一个顶点，哪些边在用它

最简单粗暴的方法就是直接定义三角形、边、顶点。

1
2
3
4
5
6
7
8
9
10
11
12
class Triangle{
    Vertex *v[3];
    Edge *e[3];
};
class Edge {
    Vertex *v[2];
    Triagle *t[2];
};
class Vertex{
    Triangle *t[];
    Edge *e[];
}

The Triangle-Neighbor Structure

三角形包含它的顶点以及它相邻三个三角形的指针。顶点包含使用它的任意一个三角形。

1
2
3
4
5
6
7
8
9
class Triangle {
    Triangle *neighbor[3];
    Vertex *v[3];
};

class Vertex {
    float x, y, z;
    Triangle *t;
}

在数组Triangle.neighbor中，第k个三角形与本三角形共享由顶点数组中的第k和第k+1个顶点所构成的边。这样构造出来的网格的结构为：

1
2
3
4
5
class Mesh{
    int tIdx[nTriangles][3]; // 每个三角形的顶点
    int tNbr[nTriangles][3]; // 每个三角形的邻三角形
    int vTri[nVertices]; // 每个顶点对应的一个毗邻的三角形
};

如果$v$是三角形$t$的第$k$个顶点，那么$v$沿着逆时针方向的下一个毗邻三角形就是t.tNbr[k]。

对于给出的一个顶点v，可以这么顺时针遍历出它所有的毗邻三角形：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function TrianglesOfVertex(v):
    tResult = {}
    t = v.t -- 其中一个毗邻三角形
    tResult.append(t)
    do:
        newT = None
        for _, ngb in t.tNbr.iteritems() do
            for __, vertex in ngb.v.iteritems() do
                # 寻找未被遍历过的三角形
                if vertex == v and (ngb not in tResult):
                    newT = ngb
                    break
            if nweT:
                break
        t = newT
        if t:
            tResult.add(t)
    while t
    return tResult

思路是先找到信息中的一个毗邻三角形，再从这个三角形的毗邻中寻找未被遍历过的、公用定点v的三角形性。由于判断了符合条件的毗邻三角形是否已经被选入结果集，所以这个遍历算法是维持着同一方向的（顺时针或逆时针）。

边翼结构

把关系信息储存在边上而不是三角形面上。

后面各种讲网格储存方式的，由于暂时在开发中用不上，所以先不看，待以后有机会涉及到光栅化了，再来看也不迟。

Scene Graphs

大多数场景组织物体都是通过使用scene graph，采用继承(hierachical)的方式。

假设有这么一个铰链钟摆，分为上下两个部分。现在要求它们转过一定角度后的位置。首先设钟摆的上半部分转交为$\theta$，并产生了位移。假设钟摆上下两部分的衔接点为b。

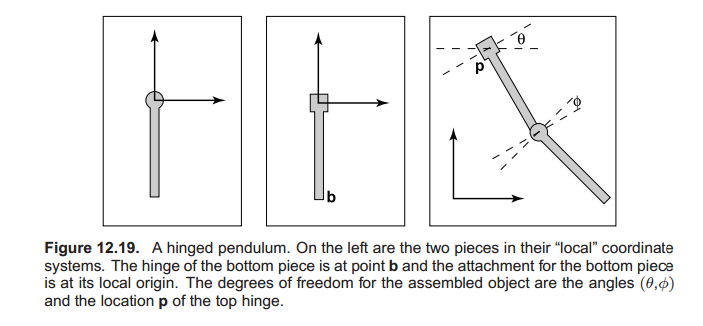
则上半部分可以表示为：

$M_1 = \text{rotate}(\theta)$

$M_2 = \text{transform(p)}$

$M_3 = M_2 M_1$

把$M_3$应用到上半部分的所有点上。

考虑下半部分的时候，由于有衔接点b，所以可以认为下半部分继承于上半部分。因故下半部分的运动可以考虑为自身的运动和上半部分运动的复合。

现在假设下半部分运动角度$\Phi$。

那么下半部分：

$M_a = \text{rotate}(\Phi)$

$M_b = \text{translate}\text{(b)}$

$M_c = M_b M_a$

$M_d = M_3 M_d$

应用$M_d$到下半部分钟摆的所有点。

transform中，步骤先的，做乘法的时候其矩阵反而在后面

结论是，子项的运动可以通过和父项的运动的矩阵相乘，来得到结果。

假设有一艘渡船，上面有一辆可以自由行驶的车。假设渡船相对于世界的运动矩阵（船的本地运动矩阵）为$M_0$，车相对于船的运动（车的本地运动矩阵）为$M_1$。那么车相对于世界的运动矩阵为$M_1 M_0$。

空间的数据结构

Buy Me A Coffee / 捐一杯咖啡的钱
分享这篇文章~
0%
//