【程序员代码面试指南】四 二叉树问题

遍历二叉树

分别用前序遍历、中序遍历和后序遍历来遍历一棵二叉树。其中：

• 前序遍历 中->左->右
• 中序遍历 左->中->右
• 后序遍历 左->右->中

分别使用递归和非递归的方法来实现。

前序遍历

递归方法：

public void PreOrderTraversal(Node root)
{
    if(root == null)
    {
        return;
    }
    System.out.println(root.value);
    PreOrderTraversal(root.left);
    PreOrderTraversal(root.right);
}

非递归方法：

使用栈的先进后出特性，让慢遍历到的先入栈（右节点先于左节点入栈）

步骤：

1. 先入栈root
2. 循环：取出栈顶，并打印，压入top.right，然后压入top.left
   直至：栈空

中序遍历

public void InOrderTraversal(Node root)
{
    if(root == null)
    {
        return;
    }
    InOrderTraversal(root.left);
    System.out.println(root.value);
    InOrderTraversal(root.right);
}

非递归方法：

还是利用栈，和前序遍历类似。

1. 循环取left节点并入栈，一直到最左
2. 取出栈顶top，打印，并拿到右节点，再次循环入栈其左节点

public static void PushAllLeftNode(Stack<Node> stack, Node root)
{
    Node cur = root;
    while(cur != null)
    {
        stack.push(cur);
        cur = cur.left;
    }
}

public static void InOrderTraversal(Node root)
{
    Stack<Node> stack = new Stack<Node>();
    PushAllLeftNode(stack, root);
    while((cur = stack.pop()) != null)
    {
        System.out.println(cur.value);
        PushAllLeftNode(stack, cur.right);
    }
}

后序遍历

public void posOrderTraversal(Node root)
{
    if(root == null)
    {
        return;
    }
    posOrderTraversal(root.left);
    posOrderTraversal(root.right);
    System.out.println(root.value);
}

打印二叉树的边界节点

给定一棵二叉树头结点head，实现二叉树边界节点的逆时针打印。

要求：

1. 头结点为边界节点之一
2. 叶节点为边界节点
3. 节点在其所在的层中是最左或最右的，也是边界节点
4. 逆时针打印，不重复打印节点

例如：

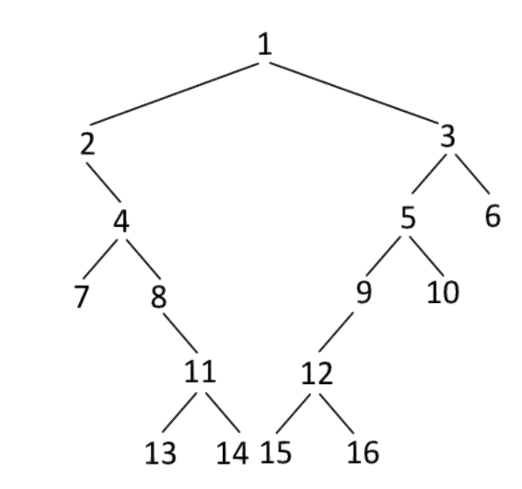
打印结果：1 2 4 7 11 13 14 15 16 12 10 6 3

实现思路

先用人话说一次。把树看成一个 三角形 ，逆时针打印，先从上往下打印最左边的节点们，也就是左边，然后打印非左边缘又非右边缘的叶节点们，也就是 底边 ，然后从下往上打印右边缘的节点们。

所以问题转化成了：首先我们要先遍历出所有的左边缘和右边缘并存储起来，这是由于

1. 我们底边的寻找条件是 非左非右 的叶节点，也就是必须先知道左边缘和右边缘
2. 右边缘的打印顺序是从下到上的，和树的遍历顺序相反，所以必须先从上往下遍历，存储起来再逆序遍历

得到左边缘和右边缘的所有节点之后，接下来就找到所有的叶节点，并且只要判断它是否存在于边缘之中，不存在就可以打印了。

打印的过程中要判断是否已经打印过，如果已经打印过就不再打印。

具体步骤

1. 得到二叉树每一层上最左和最右的节点，存到一个数组中

	最左节点	最右节点
第一层	1	1
第二层	2	3
第三层	4	6
第四层	7	10
第五层	11	12
第六层	13	16

2. 从上到下打印最左节点
3. 先序遍历二叉树，打印底边(叶节点 && 不属于最左节点 && 不属于最右节点)
4. 从下到上打印最右节点，注意如果节点同时存在于同层的最左节点之中，就不打印

在真正地写代码之前，我们先科普一下关于二叉树的几个常见操作：

获得二叉树的高度：

public int getHeight(Node h, int l) {
    if(h == null) {
        return l;
    }
    return Math.max(getHeight(h.left, l + 1), getHeight(h.right, l + 1));
}